목차
레벤슈타인 거리란?
레벤슈타인 거리는 문자열이 얼마나 비슷한 지를 나타내는 것으로 편집 거리라고도 부른다. 비슷한 어구 검색, DNA 배열의 유사성 판단 등 다양한 분야에서 활용된다.
편집할 때 몇 번의 문자열 조작이 필요한지를 계산해 편집 거리를 구한다.
예시로 살펴보자면 hat과 here의 편집거리는 3이다. hat을 here이라는 문자열로 바꾸려면 a를 e로, t를 r로 수정하고 e를 추가해야한다. 물론 hat을 here로 바꾸는 방법은 매우 다양하다. 하지만 레벤슈타인 거리는 hat에서 here로 편집할 때 필요한 문자열 조작 횟수 중에서 가장 최솟값을 말한다.
그러면 파이썬으로 레벤슈타인 거리를 구하는 프로그램을 만들어보자.
<실습 1 - 레벤슈타인 거리 구하는 프로그램>
#레벤슈타인 거리 구하기
def calc_distance(a, b):
#레벤슈타인 거리 계산
if a==b: return 0 #문자열이 동일하면 레벤슈타인 거리는 0
a_len=len(a)
b_len=len(b)
if a=="" : return b_len #문자열 a가 공집합인 경우 레벤슈타인 거리는 b_len 만큼
if b=="" : return a_len #문자열 b가 공집합인 경우 레벤슈타인 거리는 a_len 만큼
#2차원 표 (a_len+1, b_len+1) 준비하기 => 비교를 공집합부터 시작하기 때문에 '문자열 길이+1'크기의 표를 준비
matrix=[[] for i in range(a_len+1)]
for i in range(a_len+1): #0으로 초기화
matrix[i]=[0 for j in range(b_len+1)]
#0일 때 초깃값을 설정. 첫번째 행, 첫번째 열을 문자열 길이로 초기화
for i in range(a_len+1):
matrix[i][0]=i
for j in range(b_len+1):
matrix[0][j]=j
#표 채우기
for i in range(1, a_len+1):
ac=a[i-1] #비교할 문자 세팅
for j in range(1, b_len+1):
bc=b[j-1] #비교할 문자 세팅
cost=0 if (ac==bc) else 1 #비교하는 문자가 같으면 cost가 0, 다르면 1
matrix[i][j]=min([
matrix[i-1][j]+1, #문자 삽입
matrix[i][j-1]+1, #문자 제거
matrix[i-1][j-1]+cost #문자 변경
])
return matrix[a_len][b_len]
#"가나다라"와 "가마바라"의 거리
print(calc_distance("가나다라", "가마바라"))
#실행 예
samples=["신촌역", "신천군", "신천역", "신발", "마곡역"]
base=samples[0]
r=sorted(samples, key=lambda n: calc_distance(base, n))
for n in r :
print(calc_distance(base, n), n)
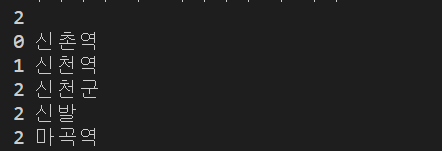
첫번째 줄은 "가나다라"와 "가마바라"의 레벤슈타인 거리다.
두번째 줄부터는 신촌역을 기준으로 잡고 다른 문자열과 레벤슈타인 거리를 구한 결과다.
프로그램의 동작 과정을 살펴보자.
1. 레벤슈타인 거리를 구하기 위해 2차원의 표를 만든다.
2. 첫행, 첫열은 문자열의 길이로 초기화해준다.
3. 표에서 빨간 부분을 채울 때,
노랑+1 : 문자 삽입
초록 + cost : 문자 변경. cost값은 비교하는 문자가 같으면 0 아니면 1이다.
파랑 +1 : 문자 삭제
이 3가지 값 중에서 최솟값이 빨간 부분에 들어가는 것이다.
이 경우에는 최솟값이 0이다. 초록 부분이 0이고, cost값은 비교하는 문자가 둘 다 '가'로 동일하기 때문에 0이다.
따라서 빨간 부분의 값은 0이다.
이렇게 계속 값을 채워나가서 마지막열, 마지막 행 부분인 회색 부분이 최종적인 레벤슈타인 거리가 된다.
| 가 | 나 | 다 | 라 | ||
| 0 | 1 | 2 | 3 | 4 | |
| 가 | 1 | ||||
| 마 | 2 | ||||
| 바 | 3 | ||||
| 라 | 4 |
표를 모두 채우면 다음과 같다.
| 가 | 나 | 다 | 라 | ||
| 0 | 1 | 2 | 3 | 4 | |
| 가 | 1 | 0 | 1 | 2 | 3 |
| 마 | 2 | 1 | 1 | 2 | 3 |
| 바 | 3 | 2 | 2 | 2 | 3 |
| 라 | 4 | 3 | 3 | 3 | 2 |
따라서 '가나다라'와 '가마바라'의 레벤슈타인 거리는 2다.
N-gram이란?
N-gram은 문자열의 유사도를 분석하는 또 다른 방법이다.
문자열을 n개의 단위로 끊어서 토큰을 생성한다. n개의 단위는 문자 n개, 단어 n개 등 사용자가 원하는 기준을 사용해 n-gram 모델을 만들면 된다.
|
앞으로 가자. 뒤로 가자. |
두 문장을 문자 3개 단위로 끊어서 토큰을 생성하면 다음과 같이 나타낼 수 있다.
['앞으로', '으로 ', '로 가', ' 가자', '가자.']
['뒤로 ', '로 가', ' 가자', '가자.']
실습 2의 방법으로 유사도를 분석하면 두 문장의 유사도는 0.6이다.
<실습2 - ngram 사용해서 유사도 분석>
#n-gram 어휘 벡터 생성
def ngram(s, num):
res=[]
slen=len(s)-num+1
for i in range(slen):
ss=s[i:i+num]
res.append(ss)
return res
#유사도 분석(빈도를 활용해서)
def diff_ngram(sa, sb, num):
a=ngram(sa, num)
b=ngram(sb, num)
r=[]
cnt=0
for i in a:
for j in b:
if i==j: #a와 b에서 동일한 토큰이 있으면 cnt+1
cnt+=1
r.append(i) #동일한 토큰을 r리스트에 추가
return cnt/len(a),r
a="오늘 강남에서 맛있는 스파게티를 먹었다."
b="강남에서 먹었던 오늘의 스파게티는 맛있었다."
#2-gram
r2, word2=diff_ngram(a, b, 2)
print("2-gram:", r2, word2)
#3-gram
r3, word3=diff_ngram(a,b,3)
print("3-gram:", r3, word3)

결과화면을 보면 유사도와 두 문장에서 동일한 토큰이 무엇인지 출력된다.
이 n-gram 모델은 문자를 기준으로 n개씩 토큰을 생성한다. 문장 a와 b의 토큰을 생성하고 같은 토큰이 존재하면 count한뒤 문장 a의 토큰 수로 나누어서 유사도를 분석했다.
참고자료
실습 : 파이썬을 이용한 머신러닝, 딥러닝 실전 개발 입문_ 쿠지라 히코우즈쿠에 저
https://lovit.github.io/nlp/2018/08/28/levenshtein_hangle/
Levenshtein (edit) distance 를 이용한 한국어 단어의 형태적 유사성
단어, 혹은 문장과 같은 string 간의 형태적 유사성을 정의하는 방법을 string distance 라 합니다. Edit distance 라는 별명을 지닌 Levenshtein distance 는 대표적인 string distance metric 중 하나입니다. 그러나 Lev
lovit.github.io
'Study > 머신러닝' 카테고리의 다른 글
| 딥러닝 학습 과정과 용어 (0) | 2021.01.11 |
|---|---|
| [6] 마르코프 체인과 LSTM으로 문장 생성하기 (0) | 2020.08.15 |
| [4] MLP(Multi Layer Perceptron)로 텍스트 분류하기 (0) | 2020.07.30 |
| [3] 나이브 베이즈 분류를 사용한 텍스트 분류 (0) | 2020.07.25 |
| [2-2] Word2Vec을 활용해 문장을 벡터로 변환하기 (0) | 2020.07.17 |

